Homework #1

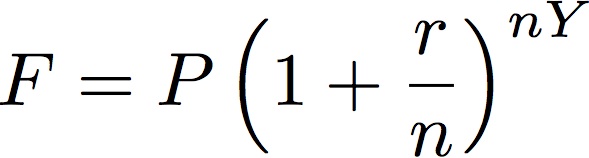
Due: January 18, 2012

Points: 100

The goal of this homework assignment is to have you write and run a Python program. The program we will use is one to compute compound interest.

We want to know how much money F will be available in Y years if we invest the principle P at rate r, compounded n times each year. The formula is:

1. (50 points) Write a program to compute the amount that $1000 will produce if invested at 8% compounded semiannually every year for 5 years. Your output is to look exactly like this:

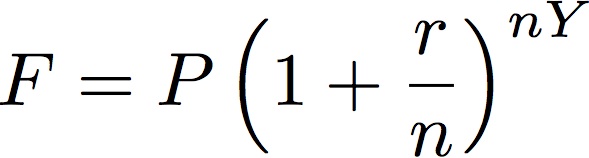
   The amount that $1000 produces when invested at 8% and compounded 2 times a year:
    1 $1081.60
    2 $1169.86
    3 $1265.32
    4 $1368.57
    5 $1480.24
   

   Call this program “cmpint1.py”.
2. (10 points) Do the same, except compound the amount daily (that is, 365 times per year). Call this program “cmpint2.py”.
3. (40 points) Now prompt the user for the principle, rate (as a percent), and number of times compounded per year. Then compute how much money will be available, just as in part 1, and print it in the same format (although with the appropriate number of lines of output).

Extra Credit

(30 points) Define the function:

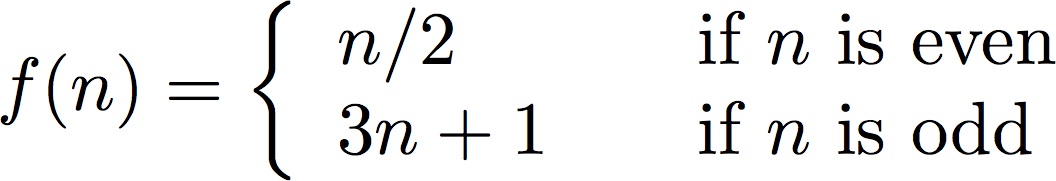
The Collatz conjecture says that, if you iterate this sequence for any initial value of n, then eventually the sequence will reach the number 1.

For a given number n, let k be the least number of iterations needed to reach the number 1 (excluding the initial value). Then k is called the total stopping time of n.

For example, if n = 29, then the sequence is:

29 88 44 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1

Write a program that takes as input a positive integer and prints both the sequence and the total stopping time for that integer. The output should look like:

29 88 44 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
The total stopping time for 29 is 18

ECS 10, Basic Concepts of Computing Winter Quarter 2012