Homework #2

Due: Wednsday, October 24, 2012 at 5:00PM
Points: 100

Please turn in your answers for the homework assignment on SmartSite, under Homework #2 in Assignments. Turn in your programs answers for the extra credit under Extra Credit #2 there.

(30 points) The program for making change presented in class (and now posted to the class web site) has one problem—poor English. Here is the output when you enter 41. As usual, what the user types is in italics and the symbol “↵” means to type a return or enter.
```
How many cents do you want me to make change for? 41↵
41 cents is 1 quarters, 1 dimes, 1 nickels, and 1 pennies
Again ('yes' for yes, anything else to stop): no↵
```
In proper English, “1” is singular, so the middle line should be:
```
41 cents is 1 quarter, 1 dime, 1 nickel, and 1 penny
```
Please fix the program so it prints out singular words (“quarter”, “dime”, “nickel”, and “penny”) when the number is 1 and the plural (“quarters”, “dimes”, “nickels”, and “pennies”) when the number is not 1 (note: in English, “0” is considered plural).
Please call your program “change1.py”.
(30 points) Write a function gcd(m, n) that calculates the greatest common divisor of m and n. The greatest divisor of m and n is the largest positive integer k that evenly divides m and n (that is, divides both of them giving a remainder of 0). Use Euclid’s algorithm to calculate this. Here is one very succinct way to describe the algorithm (as usual in Python, m % n is the remainder of m when divided by n):

Repeatedly replace m with n, and n with m % n, until n is 0

italics

First number (0 to stop): 113↵
Second number: 293↵
The greatest common divisor of 293 and 113 is 1
First number (0 to stop): 14↵
Second number: 18↵
The greatest common divisor of 18 and 14 is 2
First number (0 to stop): -30↵
Second number: -66↵
The greatest common divisor of -66 and -30 is 6
First number (0 to stop): 7↵
Second number: 0↵
The greatest common divisor of 0 and 7 is 7
First number (0 to stop): 0↵

Please call your program “gcd.py”.

(40 points) Define the mathematical function: The Collatz conjecture says that, if you iterate this sequence for any initial value of n, then eventually the sequence will reach the number 1.
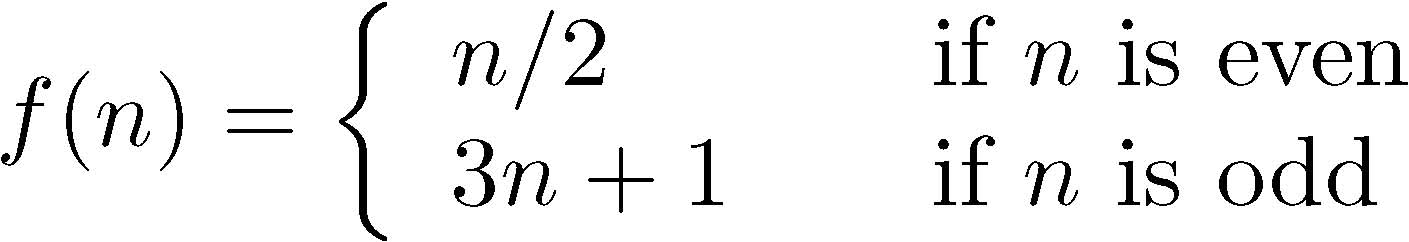
For a given number n, let k be the least number of iterations needed to reach the number 1 (excluding the initial value). Then k is called the total stopping time of n.
For example, if n = 29, then the sequence is:
```
29 88 44 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
```
and so the total stopping time of 29 is 18.
Write a program that takes as input a positive integer and prints both the sequence and the total stopping time for that integer. The output should look like:
```
29 88 44 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
The total stopping time for 29 is 18
```
Please call your program “collatz.py”.

Extra Credit

Remember to hand this in under Extra Credit #2, not under Homework #2!

(30 points) Consider the following output from the answer to problem 1:
```
How many cents do you want me to make change for? 30↵
30 cents is 1 quarter, 0 dimes, 1 nickel, and 0 pennies
Again (’yes' for yes, anything else to stop): no↵
```
The more natural way to say the middle line is:
```
30 cents is 1 quarter and 1 nickel
```
In other words, the coins of which 0 are to be given should not appear in the output. Please fix your answer to problem 1 not to print those coins that the user would not get. Your punctuation should be correct, and don’t forget to use the word “and” if you have more than one type of coin!
Please call your program “change2.py”.

A PDF version is available here.

ECS 10, Basic Concepts of Computing
Fall Quarter 2012