Homework #3

Due: Friday, November 9, 2012 at 5:00PM
Points: 100

Please turn in your answers for the homework assignment on SmartSite, under Homework #3 in Assignments. Turn in your programs answers for the extra credit under Extra Credit #3 there.

(30 points) The sign or signum function sgn(x) is a mathematical function that returns the sign of x:

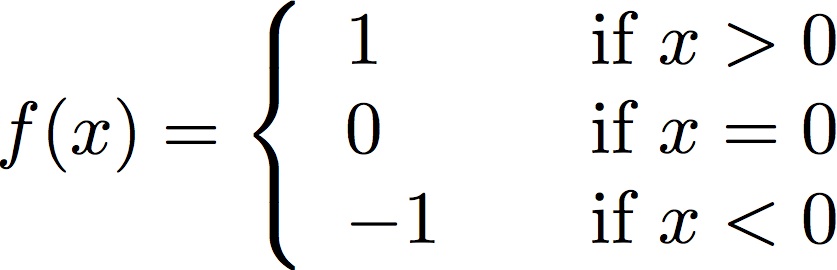
Please write a program that requests a real (floating point) number x and computes sgn(x). The program must continue to do so until the user types an end-of-file (that is, control-D). Your output should look like:
```
Please enter a number: -2.71828↵
sgn(-2.72) =  -1
Please enter a number: 3.14159↵
sgn(3.14) =  1
Please enter a number: 0↵
sgn(0.00) =  0
Please enter a number: 42↵
sgn(42.00) =  1
Please enter a number: -999↵
sgn(-999.00) =  -1
Please enter a number: control-D
```
To type control-D, hold down the control key and type the D key. Nothing will appear visibly.
Please call your program “sgn.py”.
(70 points) This program asks you to approximate the square root of a number using a technique called Newton’s method. This problem is adapted from the “Project: Newton's Method” section of the textbook on p. 47.
1. The algorithm for Newton’s method for computing the square root of k is:
      Make an initial guess x for the square root (for example, take half of k)
      Repeat until desired accuracy is reached:
          Replace the guess x with the average of x and k/x
  
  For example, to compute the square root of 2, you would proceed as follows:
      Guess x = 2/2 = 1
      First iteration: x = (x + 2/x)/2 = (1 + 2/1)/2 = 1.5
      Second iteration: x = (x + 2/x)/2 = (1.5 + 2/1.5)/2 = 1.416667
      Third iteration: x = (x + 2/x)/2 = (1.416667 + 2/1.416667)/2 = 1.414216
  Write a function called newton to do this. Your function will take one argument, the number whose square root is to be computed. If that number is negative, it should raise a ValueError exception, with the message “Cannot take the square root of a negative number”. Otherwise, it should use Newton’s method to compute the approximation of the square root of the argument accurate to 5 decimal places.
  Hint: As you don’t know what the actual square root is, you technically don’t know when it is accurate to 5 decimal places. But you do know the square of the actual square root of k; it’s simply k. So, each time you iterate, compute the (absolute value of) the difference between the square of your guess and k; if it is less than (10^-5)² = 10^-10, you are as accurate as needed!
2. Write a program that calls your function. That program is to prompt the user for a number, and print both the approximate square root computed using Newton’s method (your function) and the absolute value of the difference between that approximation and the actual square root as computed using the math library. Your output is to look like this:
```
Number? 200↵
The approximate square root of 200.0 is 14.1421356237
The error is 3.5527136788e-15
```
  Your program is to read one number and stop (that is, it should not loop and ask for another). Handle EOF and input errors properly, using try . . . except. Here is some more sample output:
```
Number? 15↵
The approximate square root of 15.0 is 3.87298334621
The error is 8.881784197e-16
```
```
Number? hello↵
Could not convert string to float: 'hello'
```
```
Number? -16↵
Cannot take the square root of a negative number
```
```
Number? control-D
```
Please call your program “newton.py”.

Extra Credit

Remember to hand this in under Extra Credit #3, not under Homework #3!

(40 points) This program asks you to plot four functions over specified intervals. To plot these, begin at the starting point of the interval, and advance 0.01 until you reach the end.
The four functions are in the file “funcs.py” available in the assignment area. The intervals they are to be plotted over are:

function      intervals on x axis

f1      [-7, -3]; [-1, 1]; [3, 7]

f2      [-7, -4]; [4, 7]

f3      [-4, 4]

f4      [-3, -1]; [1, 3]

You do not need to draw the axes. Also, set the speed of the turtle (pen) to 10; otherwise, drawing the picture will take a long time.
What picture does this draw?
Please call your program “plotting.py”.
Hint: If you don’t scale the x and y co-ordinates of the plot, the figure will probably be too small to see it well. I used a scale factor of 25—that is, when I plotted or moved to point (x, y), I multiplied both x and y by 25 before plotting or moving to it. Also, you will need to import the square root function for the functions to work:
```
from math import sqrt
```

A PDF version is available here.

ECS 10, Basic Concepts of Computing
Fall Quarter 2012

function		intervals on x axis
`f1`		[-7, -3]; [-1, 1]; [3, 7]
`f2`		[-7, -4]; [4, 7]
`f3`		[-4, 4]
`f4`		[-3, -1]; [1, 3]