Homework #1

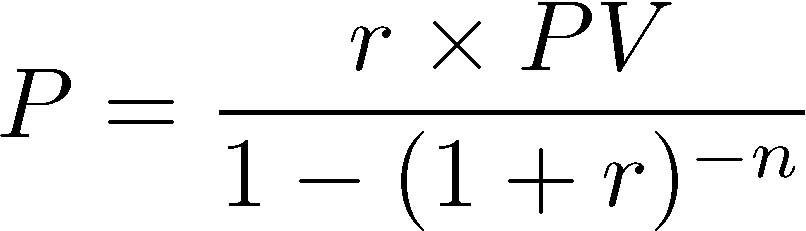
If you have not already taken out a loan, you undoubtedly will some time in your life. For example, when you buy a house, the “mortgage” you pay is simply payment on the amount that the mortgage holder has loaned you. If you have a loan to pay your school bills, at some point you will have to repay it. This program will help you figure out how much you will need to pay per month, assuming the loan is a standard one.

Three quantities define how much a borrower has to pay per month:

• PV, the amount borrowed (this is called the “present value”). If you borrowed $200,000.00, then PV is $200,000.00.
• r, the interest rate per period. For example, if your loan’s interest is 6.5% per year, and you are paying monthly, this would be 6.5%/12. If you are paying every two weeks, r would be 6.5%/26, because there are 26 two-week periods in a year.
• n, the number of periods. If you have a 5 year loan with monthly payments, then n = 5 × 12 = 60. If you pay biweekly, then n = 5 × 26 = 130.

The formula for the monthly payment, which does not change throughout the repaying of the loan is:

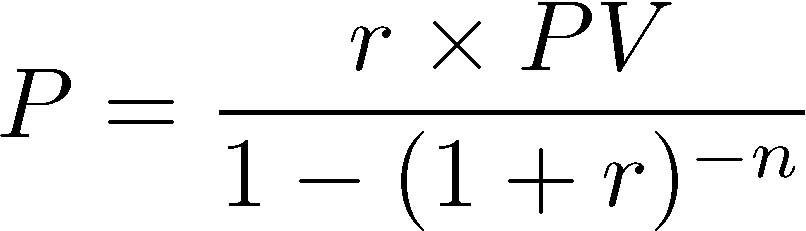
The amount of principle that is left to be repaid after m months is:

1. (50 points) Assume the loan is to be repaid in monthly payments. The amount borrowed is $5,000.00. The annual interest rate is 6.5%. The period of the loan is 1 year. Write a program that computes and prints the month, payment, and remaining principle for each payment.
   Input. This program takes no input.
   Output. Your program’s output should look exactly like this:

   Payment schedule for a loan of $5000.00 at 6.5% interest, repaid over 1 year:
   month payment remaining
      1   431.48   4595.60
      2   431.48   4189.01
      3   431.48   3780.22
      4   431.48   3369.21
      5   431.48   2955.98
      6   431.48   2540.51
      7   431.48   2122.79
      8   431.48   1702.81
      9   431.48   1280.55
     10   431.48    856.00
     11   431.48    429.16
     12   431.48      0.00
   

   Submit. Name your program “loan1.py” and submit it to the Homework #1 area for this class on SmartSite.

2. (50 points) Now change the program you just wrote to ask the user for the loan amount, the annual interest rate, and the number of years in the period of the loan. It then must compute and print the month, payment, and remaining principle for each payment.
   Input. The sequence of prompts for your program must exactly match the following (the red text is what you type):

   What is the annual interest rate (enter it without the % sign)? 6.5
   How much is being borrowed (no commas)? 5000
   How many years is the loan for? 1
   

   Output. The output of your program must look exactly like this:

   Payment schedule for a loan of $5000.00 at 6.5% interest, repaid over 1 years:
   month payment remaining
      1   431.48   4595.60
      2   431.48   4189.01
      3   431.48   3780.22
      4   431.48   3369.21
      5   431.48   2955.98
      6   431.48   2540.51
      7   431.48   2122.79
      8   431.48   1702.81
      9   431.48   1280.55
     10   431.48    856.00
     11   431.48    429.16
     12   431.48      0.00
   

   Submit. Name your program “loan2.py” and submit it to the Homework #1 area for this class on SmartSite.

Hint: The print statement for the lines in the table after the second is:

print(" %3d  %7.2f %9.2f" % (m, P, RP))