Homework #2

The Monty Hall problem is a very famous problem in probability. It’s based on an old TV show called “Let’s Make a Deal”. The stage of that show had 3 doors numbered “1”, “2”, and “3”. Behind one of the doors was a valuable prize (like a new car); the other two contained gag gifts (like a goat or a can of cat food). The host, Monty Hall (hence the name of the problem), would choose someone from the audience and ask them to pick a door. The contestant would choose one, say door “2”. Monty would then open one of the other doors that always had a gag gift behind it (say, door “1” for our example). He would then ask the contestant if he or she wanted to stay with door “2”, or change their selection to door “3”. The problem is to determine which action — keep or change — gives the contestant the greater probability of selecting the door with the real prize.

We’re going to answer this question by simulation — the technique is called a Monte Carlo method. Basically, we play a large number of games on the computer, always switching doors (or never switching doors), and record whether we won. We then divide the number of times we won by the number of trials, giving a number between 0 and 1 (inclusive). This is the probability that the strategy will cause the contestant to win.

We’re going to build this program in steps, because that will simplify writing it.

1. (30 points) First, we will write functions to simulate playing one game. The basic approach is to generate a random number representing the door behind which the real prize sits, and another random number representing the door that the contestant initially selects. Monty opens the remaining door. Then, have the contestant switch doors (or not switch doors), and see if the contestant winds up with the door behind which the prize sits.

   Write two different functions to do this. The first, called montyalways(), has the contestant always changing doors after Monty opens the third door. The second, called montynever(), has the contestant never changing doors after Monty opens the third door. Both functions should return the Boolean value True if the contestant wins, and the Boolean False if she does not.

   Input. None.

   Output. None; the function returns True or False depending on whether the contestant wins or does not win.

   Submit. Name your file “monty1.py” and submit it to the Homework #2 area for this class on SmartSite.

   Hint: Before you start programming, think about the best approach for these functions. There is a very simple way to do them.

2. (20 points) Now we will simulate a large number of games. Write a program that asks the user for the number of games to be played. Then play one set of games for the contestant always changing the door and another set for the contestant never changing the door. Print the resulting (decimal) fraction of times that the contestant wins, and the number of games won.

   Input. The number of games to be played. This must be a positive integer. Remember to handle invalid inputs gracefully, by printing an error message and exiting the program.

   Here is what a correct input should look like: (the red text is what you type):

   
   Number of games to play: 100000
   

   If the input is invalid:

   
   Number of games to play: hello
   Please enter a positive integer
   

   and then the program exits.

   Output. The output of your program must look like this:

   
   Out of 100000 games:
   Always switching wins:  0.6680600 (66806 games)
   Never switching wins:  0.3346300 (33463 games)
   

   Important note: your numbers may be different.

   Submit. Name your file “monty2.py” and submit it to the Homework #2 area for this class on SmartSite.

3. (50 points) Now we will add a graphical output to visualize the results. This is a common practice in science and engineering, because the eye helps you understand the results faster than studying columns of numbers. We will draw a histogram, with the bars being the relative sizes of the numbers.

   Your histogram should look like this:

   

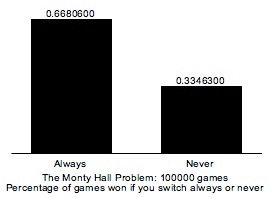
   To do this drawing, I scaled all co-ordinates by 2, and shifted the origin to (−60, −60) (in other words, the point (0, 0) was plotted as ((0−60) × 2, (0−60) × 2) or (−120, −120); the point (115, 35) was plotted as ((115−60) × 2, (35−60) × 2) or (−55 × 2, −25 × 2), or (−110, −50)); this centered the picture better. The length of the bottom line is 125 units (before scaling); each bar of the histogram is 40 units wide, with 10 units on either side and 25 units between them (again, before scaling). The text above and below each bar is centered over and under the bar; the top one is 0 units above the bar, and the bottom one is −8 units below the bar (before scaling). The text is also centered below the full horizontal line; the top line of the text is 15 units below the line (before scaling), and the bottom line of the text is 20 units below the line (before scaling). The font is Ariel 10-point normal. So if your turtle is called “yertle”, the write statement for the bottom line would be:

   
   yertle.write("Percentage of games won if you switch always or never",
                False, "center", ("Arial", 10, "normal"))
   

   The input and output should be the same as for “monty2.py”, except that you must also draw the histogram.

   Submit. Name your file “monty3.py” and submit it to the Homework #2 area for this class on SmartSite.