Improper Nesting Example

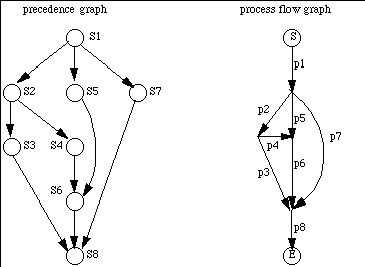
One of the limits on the use of parbegin/parend, and any related constructs, is that the program involved must be properly nested. Not all programs are. For example, consider the program represented by the following graphs.

The Program as Graphs

Using fork/join Primitives

The program equivalent to these precedence and process flow graphs is:

    t6 := 2;
    t8 := 3;
    S1; fork p2; fork p5; fork p7; quit;
p2: S2; fork p3; fork p4; quit;
p5: S5; join t6, p6; quit;
p7: S7; join t8, p8; quit;
p3: S3; join t8, p8; quit;
p4: S4; join t6, p6; quit;
p6: S6; join t8, p8; quit;
p8: S8; quit

where S_i is the program for p_i.

Using parbegin/parend Primitives

To see if this is possible, we must determine if the above program is properly nested. If not, we clearly cannot represent it using parbegin and parend, which require a block structure, and hence proper nesting.

Let S(a,b) represent the serial execution of processes a and b, and P(a,b) the parallel execution of processes a and b. Then a process flow graph is properly nested if it can be described by P, S, and functional composition. For example, the program

parbegin
  p1:a := b + 1;
  p2:c := d + 1;
parend
p3:e := a + c;

would be written as

S(P(p₁, p₂), p₃)

We now prove:

Claim: The example is not properly nested.
Proof: For something to be properly nested, it must be of the form S(p_i, p_j) or P(p_i, p_j) at the most interior level. Clearly the example’s most interior level is not P(p_i, p_j) as there are no constructs of that form in the graph. In the graph, all serially connected processes p_i and p_j have at least 1 more process p_k starting or finishing at the node n_ij between p_i and p_j; but if S(p_i, p_j) is in the innermost level, there can be no such p_k (else a more interior P or S is needed, contradiction). Hence, it is not S(p_i, p_j) either.