Distributed Systems Fundamentals

1. Distributed system?
   1. What is it?
   2. Why use it?
2. System Architectures
   1. minicomputer model
   2. workstation model
   3. processor pool
3. Issues
   1. global knowledge
   2. naming
   3. scalability
   4. compatibility
   5. process synchronization, communication
   6. security
   7. structure
4. Networks
   1. goals
   2. message, packet, subnet, session
   3. switching: circuit, store-and-forward, message, packet, virtual circuit, dynamic routing
   4. OSI model: PDUs, layering
      1. physical: ethernet, aloha, etc.
      2. data link layer: frames, parity checks, link encryption
      3. network layer: virtual circult vs. datagram, routing via flooding, static routes, dynamic routes, centralized routing vs. distributed routing; congestion solutions (packet discarding, isarithmic, choke packets)
      4. transport: services provided (UDP vs. TCP), functions to higher layers, addressing schemes (flat, DNS, etc.), gateway fragmentation and reassembly
      5. session: adds session characteristics like authentication
      6. presentation: compression, end-to-end encryption, virtual terminal
      7. application: user-level programs
5. Clocks
   1. happened-before relation
   2. Lamport's distributed clocks: a -> b means C(a) < C(b)
   3. Example where C(a) < C(b) does not mean a -> b
   4. Vector clocks and causal relation
   5. ordering of messages so you receive them in the order sent
      1. why
      2. for broadcast (ISIS): Birman-Schiper-Stephenson
      3. for point to point: Schiper-Eggli-Sandoz
6. Global state
   1. Show problem of slicing state when something is in transit
   2. Define local state; send(m_ij) IN LS_i iff time of send(m_ij) < current time of LS_i; similar for receive
   3. transit(LS_i, LS_j); inconsistent(LS_i, LS_j); consistent state is one with inconsistent set empty for all pairs LS_i, LS_j
   4. Consistent global state: Chandry-Lamport
7. Termination detection
   1. Haung

Lamport's Clocks

Introduction

Lamport's clocks keep a virtual time among distributed systems. The goal is to provide an ordering upon events within the system.

Notation

• P_i process
• C_i clock associated with process P_i

Protocol

1. Increment clock C_i between any two successive events in process P_i: C_i <- C_i + d (d > 0)
2. Let event a be the sending of a message by process P_i; it is given the timestamp t^a = C(a). Let b be the receipt of that message by P_j. Then when P_j receives the message, C_j <- max(C_j, t^a) + d (d > 0)

Example

Assume all clocks start at 0, and d is 1 (that is, each event incrememts the clock by 1). At event e12, C₁(e12) = 2. Event e12 is the sending of a message to P₂. When P₂ receives the message (event e23), its clock C₂ = 2. The clock is reset to 3. Event e24 is P₂'s sending a message to P₃. That message is received at e32. C₃ is 1 (as one event has passed). By rule 2, C₃ is reset to the maximum of C₂(e24)+1 and the current value of C₃, so C₃ becomes 5.

Problem

Clearly, if a -> b, then C(a) < C(b). But if C(a) < C(b), does a -> b?

The answer, surprisingly, is not necessarily. In the above example, C₃(e31) = 1 < 2 = C₁(e12). But e31 and e12 are causally unrelated; that is, e31 ->X e12. However, C₁(e11) < C₃(e32), and clearly e11 -> e32. Hence one cannot say one way or the other.

Vector Clocks

Introduction

This is based upon Lamport's clocks, but each process keeps track of what is believes the other processes' interrnal clocks are (hence the name, vector clocks). The goal is to provide an ordering upon events within the system.

Notation

• n processes
• P_i process
• C_i vector clock associated with process P_i; jth element is C_i[j] and contains P_i's latest value for the current time in process P_j

Protocol

1. Increment clock C_i between any two successive events in process P_i: C_i[i] <- C_i[i] + d (d > 0)
2. Let event a be the sending of a message by process P_i; it is given the vector timestamp t^a = Ci(a). Let b be the receipt of that message by P_j. Then when P_j receives the message, it updates its vector clock for all k = 1, ..., n: C_j[k] <- max(C_j[k], t^a[k] + d) (d > 0)

Example

Here is the progression of time for the three processes:

e11: C₁ = (1, 0, 0)
e31: C₃ = (0, 0, 1)
e21: C₂ = (0, 0, 1) as t^a = C₃(e31) = (0, 0, 1) and previously, C₃ was (0, 0, 1)
e22: C₂ = (0, 1, 1)
e12: C₁ = (2, 0, 0)
e23: C₂ = (2, 1, 1) as t^a = C₁(e12) = (2, 0, 0) and previously, C₂ was (0, 1, 1)
e24: C₂ = (2, 2, 1)
e13: C₁ = (2, 1, 1) as t^a = C₂(e22) = (0, 1, 1) and previously, C₁ was (2, 0, 0)
e32: C₃ = (2, 2, 1) as t^a = C₂(e24) = (2, 2, 1) and previously, C₃ was (0, 0, 1)

Notice that C₁(e11) < C₃(e32), so e11 -> e32, but C₁(e11) and C₃(e31) are incomparable, so e11 and e31 are concurrent.

Birman-Schiper-Stephenson Protocol

Introduction

The goal of this protocol is to preserve ordering in the sending of messages. For example, if send(m₁) -> send(m₂), then for all processes that receive both m₁ and m₂, receive(m₁) -> receive(m₂). The basic idea is that m₂ is not given to the process until m₁ is given. This means a buffer is needed for pending deliveries. Also, each message has an associated vector that contains information for the recipient to determine if another message preceded it. Also, we shall assume all messages are broadcast. Clocks are updated only when messages are sent.

Notation

• n processes
• P_i process
• C_i vector clock associated with process P_i; jth element is C_i[j] and contains P_i's latest value for the current time in process P_j
• t^m vector timestamp for message m (stamped after local clock is incremented)

Protocol

P_i sends a message to P_j

1. P_i increments C_i[i] and sets the timestamp t^m = C_i[i] for message m.

P_j receives a message from P_i

1. When P_j, j != i, receives m with timestamp t^m, it delays the message's delivery until both:
   1. C_j[i] = t^m[i] - 1; and
   2. for all k <= n and k != i, C_j[k] <= t^m[k].
2. When the message is delivered to P_j, update P_j's vector clock
3. Check buffered messages to see if any can be delivered.

Example

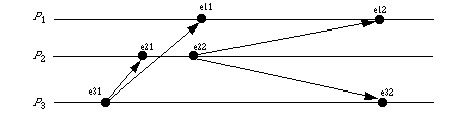
Here is the protocol applied to the above situation:

e31: P₃ sends message a; C₃ = (0, 0, 1); t^a = (0, 0, 1)
e21: P₂ receives message a. As C₂ = (0, 0, 0), C₂[3] = t^a[3] - 1 = 1 - 1 = 0 and C₂[1] => t^a[1] and C₂[2] => t^a[2] = 0. So the message is accepted, and C₂ is set to (0, 0, 1)
e11: P₁ receives message a. As C₁ = (0, 0, 0), C₁[3] = t^a[3] - 1 = 1 - 1 = 0 and C₁[1] => t^a[1] and C₁[2] => t^a[2] = 0. So the message is accepted, and C₁ is set to (0, 0, 1)
e22: P₂ sends message b; C₂ = (0, 1, 1); t^b = (0, 1, 1)
e12: P₁ receives message b. As C₁ = (0, 0, 1), C₁[2] = t^b[2] - 1 = 1- 1 = 0 and C₁[1] => t^b[1] and C₁[3] => tb[2] = 0. So the message is accepted, and C₁ is set to (0, 1, 1)
e32: P₃ receives message b. As C₃ = (0, 0, 1), C₃[2] = t^b[2] - 1 = 1 - 1 = 1 and C₁[1] => t^b[1] and C₁[3] => tb[2] = 0. So the message is accepted, and C₃ is set to (0, 1, 1)

Now, suppose t^a arrived as event e12, and t^b as event e11. Then the progression of time in P₁ goes like this:

e11: P₁ receives message b. As C₁ = (0, 0, 0), C₁[2] = t^b[2] - 1 = 1 - 1 = 0 and C₁[1] => t^b[1], but C₁[3] < t^b[3], so the message is held until another message arrives. The vector clock updating algorithm is not run.
e12: P₁ receives message a. As C₁ = (0, 0, 0), C₁[3] = t^a[3] - 1 = 1 - 1 = 0, C₁[1] => t^a[1], and C₁[2] => t^a[2]. The message is accepted and C₁ is set to (0, 0, 1). Now the queue is checked. As C₁[2] = t^b[2] - 1 = 1 - 1 = 0, C₁[1] => t^b[1], and C₁[3] => t^b[3], that message is accepted and C₁ is set to (0, 1, 1).

Schiper-Eggli-Sandoz Protocol

Introduction

The goal of this protocol is to ensure that messages are given to the receiving processes in order of sending. Unlike the Birman-Schiper-Stephenson protocol, it does not require using broadcast messages. Each message has an associated vector that contains information for the recipient to determine if another message preceded it. Clocks are updated only when messages are sent.

Notation

• n processes
• P_i process
• C_i vector clock associated with process P_i; jth element is C_i[j] and contains P_i's latest value for the current time in process P_k
• t^m vector timestamp for message m (stamped after local clock is incremented)
• tⁱ current time at process P_i
• V_i vector of P_i's previously sent messages; V_i[j] = t^m, where P_j is the destination process and t^m the vector timestamp of the message; V_i[j][k] is the kth component of V_i[j].
• V^m vector accompanying message m

Protocol

P_i sends a message to P_j

1. Pi sends message m, timestamped t^m, and V_i, to process P_j
2. Pi sets V_i[j] = t^m

P_j receives a message from P_i

1. When P_j, j != i, receives m, it delays the message's delivery if both:
   1. V^m[j] is set; and
   2. V^m[j] < t^j
2. When the message is delivered to P_j, update all set elements of V_j with the corresponding elements of V^m, except for V_j[j], as follows:
   1. If V_j[k] and V^m[k] are uninitialized, do nothing.
   2. If V_j[k] is uninitialized and V^m[k] is initialized, set V_j[k] = V^m[k].
   3. If both V_j[k] and V^m[k] are initialized, set V_j[k][k'] = max(V_j[k][k'], V^m[k][k']) for all k' = 1, ..., n
3. Update P_j's vector clock.
4. Check buffered messages to see if any can be delivered.

Example

Here is the protocol applied to the above situation:

e31: P₃ sends message a to P₂. C₃ = (0, 0, 1); t^a = (0, 0, 1), V^a = (?, ?, ?); V₃ = (?, (0, 0, 1), ?)
e21: P₂ receives message a from P₁. As V^a[2] is uninitialized, the message is accepted. V₂ is set to (?, ?, ?) and C₂ is set to (0, 0, 1).
e22: P₂ sends message b to P₁. C₂ = (0, 1, 1); t^b = (0, 1, 1), V^b = (?, ?, ?); V₂ = ((0, 1, 1), ?, ?)
e11: P₁ sends message c to P₃. C₁ = (1, 0, 0); t^c = (1, 0, 0), V^c = (?, ?, ?); V₁ = (?, ?, (1, 0, 0))
e12: P₁ receives message b from P₂. As V^b[1] is uninitialized, the message is accepted. V₁ is set to (?, ?, ?) and C₁ is set to (1, 1, 1).
e32: P₃ receives message c from P₁. As V^c[3] is uninitialized, the message is accepted. V₃ is set to (?, ?, ?) and C₃ is set to (1, 0, 1).
e23: P₂ sends message d to P₁. C₂ = (0, 2, 1); t^d = (0, 2, 1), V^d = ((0, 1, 1), ?, ?); V₂ = ((0, 2, 1), ?, (0, 0, 1))
e13: P₁ receives message d from P₂. As Vd[1] < C₁[1], so the message is accepted. V₁ is set to ((0, 1, 1), ?, ?) and C₁ is set to (1, 2, 1).

Now, suppose t^b arrived as event e13, and t^d as event e12. Then the progression in P₁ goes like this:

e12: P₁ receives message d from P₂. But V^d[1] = (0, 1, 1) <X (1, 0, 0) = C₃, so the message is queued for later delivery.
e13: P₁ receives message b from P₂. As V^b[1] is uninitialized, the message is accepted. V₁ is set to (?, ?, ?) and C₁ is set to (1, 1, 1). The message on the queue is now checked. As V^d[1] = (0, 1, 1) < (1, 1, 1) = C₁, the message is now accepted. V₁ is set to ((0, 1, 1), ?, ?) and C₁ is set to (1, 2, 1).

Chandy-Lamport Global State Recording Protocol

Introduction

The goal of this distributed algorithm is to capture a consistent global state. It assumes all communication channels are FIFO. It uses a distinguished message called a marker to start the algorithm.

Protocol

P_i sends marker

1. P_i records its local state LS_i
2. For each C_ij on which P_i has not already sent a marker, P_i sends a marker before sending other messages.

P_i receives marker from P_j

1. If P_i has not recorded its state:
   1. Record the state of C_ji as empty
   2. Send the marker as described above
2. If P_i has recorded its state LS_i
   1. Record the state of C_ji to be the sequence of messages received between the computation of LS_i and the marker from C_ji.

Example

Here, all processes are connected by communications channels C_ij. Messages being sent over the channels are represented by arrows between the processes.

Snapshot s₁:

P₁ records LS₁, sends markers on C₁₂ and C₁₃
P₂ receives marker from P₁ on C₁₂; it records its state LS₂, records state of C₁₂ as empty, and sends markers on C₂₁ and C₂₃.
P₃ receives marker from P₁ on C₁₃; it records its state LS₃, records state of C₁₃ as empty, and sends markers on C₃₁ and C₃₂.
P₁ receives marker from P₂ on C₂₁; as LS₁ is recorded, it records the state of C₂₁ as empty.
P₁ receives marker from P₃ on C₃₁; as LS₁ is recorded, it records the state of C₃₁ as empty.
P₂ receives marker from P₃ on C₃₂; as LS₂ is recorded, it records the state of C₃₂ as empty.
P₃ receives marker from P₂ on C₂₃; as LS₃ is recorded, it records the state of C₂₃ as empty.

Snapshot s₂: now a message is in transit on C12 and C21.

P₁ records LS₁, sends markers on C₁₂ and C₁₃
P₂ receives marker from P₁ on C₁₂ after the message from P₁ arrives; it records its state LS₂, records state of C₁₂ as empty, and sends marker on C₂₁ and C₂₃
P₃ receives marker from P₁ on C₁₃; it records its state LS₃, records state of C₁₃ as empty, and sends markers on C₃₁ and C₃₂.
P₁ receives marker from P₂ on C₂₁; as LS₁ is recorded, and a message has arrived since LS₁ was recorded, it records the state of C₂₁ as containing that message.
P₁ receives marker from P₃ on C₃₁; as LS₁ is recorded, it records the state of C₃₁ as empty.
P₂ receives marker from P₃ on C₃₂; as LS₂ is recorded, it records the state of C₃₂ as empty.
P₃ receives marker from P₂ on C₂₃; as LS₃ is recorded, it records the state of C₂₃ as empty.

Huang's Termination Detection Protocol

Introduction

The goal of this protocol is to detect when a distributed computation terminates.

Notation

• n processes
• P_i process; without loss of generality, let P₀ be the controlling agent
• W_i weight of process P_i; initially, W₀ = 1 and for all other i, W_i = 0.
• B(W) computation message with assigned weight W
• C(W) control message sent from process to controlling agent with assigned weight W

Protocol

P_i sends a computation message to P_j

1. Set W_i' and W_j to values such that W_i' + W_j = W_i, W_i > 0, W_j > 0. (W_i' is the new weight of P_i.)
2. Send B(W_j) to P_j

P_j receives a computation message B(W) from P_i

1. W_j <- W_j + W
2. If P_j is idle, P_j becomes active

P_i becomes idle

1. Send C(W_i) to P₀
2. W_i = 0
3. P_i becomes idle

P_i receives a control message C(W)

1. W_i <- W_i + W
2. If W_i = 1, the computation has completed.

Example

The picture shows a process P₀, designated the controlling agent, with W₀ = 1. It asks P₁ and P₂ to do some computation. It sets W₁ to 0.2, W₂ to 0.3, and W₃ to 0.5. P₂ in turn asks P₃ and P₄ to do some computations. It sets W₃ to 0.1 and W₄ to 0.1.

When P₃ terminates, it sends C(W₃) = C(0.1) to P₂, which changes W₂ to 0.1 + 0.1 = 0.2.

When P₂ terminates, it sends C(W₂) = C(0.2) to P₀, which changes W₀ to 0.5 + 0.2 = 0.7.

When P₄ terminates, it sends C(W₄) = C(0.1) to P₀, which changes W₀ to 0.7 + 0.1 = 0.8.

When P₁ terminates, it sends C(W₁) = C(0.2) to P₀, which changes W₀ to 0.8 + 0.2 = 1.

P₀ thereupon concludes that the computation is finished.

Total number of messages passed: 8 (one to start each computation, one to return the weight).