Process Synchronization and Cooperation
- Parallelism
- concurrent vs. sequential
- logical vs. physical concurrency
- process creation: static vs. dynamic
- Proper nesting
- S, P
- definition of proper nesting
- precedence graph
- Precedence relation <
- predecessor process
- proces domain, range
- equivalent systems of processes
- determinate system of processes
- Bernstein conditions
- mutually non-interfering system
- Theorem: mutually noninterfering systems are determinate
- maximally parallel system
- Basic concurrency language constructs
- cobegin/coend
- fork/join/quit
- Critical section problems
- producer consumer
- readers writers; first gives readers priority, second gives writers
priority
- dining philosophers
- Software solutionss
- Dekker's, Peterson's
- bakery algorithm
- Hardware solutionss
- disable interrupts
- test and set
- Basic language constructs
- semaphores
- sequencers and eventcounters
- simultamepus primitives SP, SV, P-or
- send reveive
- Higher-level language constructs
- abstract data types
- comparison of constructs: constraints, expressive power, ease of use,
portability, process failure
- monitors
- crowd monitors
- invariant expressions
- path expressions
- predicate path expressions
- CSP
- RPC
- ADA(TM)
Improper Nesting Example
Introduction
One of the limits on the use of parbegin/parend, and any related constructs, is
that the program involved must be properly nested. Not all programs are. For
example, consider the program represented by the following graphs.
The Program as Graphs
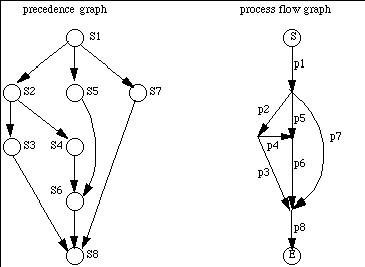
Using fork/join Primitives
The program equivalent to these precedence and process flow graphs is:
t6 := 2;
t8 := 3;
S1; fork p2; fork p5; fork p7; quit;
p2: S2; fork p3: fork p4; quit;
p5: S5; join t6, p6; quit;
p7: S7; join t8, p8; quit;
p3: S3; join t8, p8; quit;
p4: S4; join t6, p6; quit;
p6: S6; join t8, p8; quit;
p8: S8; quit
where Si is the program for pi.
Using parbegin/parend Primitives
To see if this is possible, we must determine if the above program is properly
nested. If not, we clearly cannot represent it using parbegin and
parend, which require a block structure, and hence proper nesting.
Let S(a,b) represent the serial execution of processes
a and b, and P(a,b) the parallel execution
of processes a and b. Then a process flow graph is properly
nested if it can be described by P, S, and functional
composition. For example, the program
parbegin
p1: a := b + 1;
p2: c := d + 1;
parend
p3: e := a + c;
would be written as
S(P(p1,p2),p3)
We now prove:
Claim. The example is not properly nested.
Proof: For something to be properly nested, it must be of the form
S(pi,pj) or P(pi,pj) at the most
interior level.
Clearly the example's most interior level is not P(pi,pj)
as there are no constructs of that form in the graph.
In the graph, all serially connected processes pi and pj have at least 1 more
process pk starting or finishing at the node nij between
pi and pj; but if S(pi,pj) is in the
innermost level, there can be no such pk (else a more interior P
or S is needed, contradiction). Hence, it's not
S(pi,pj)) either.
Maximally Parallel Systems
Introduction
A maximally parallel system is a determinate system for which the
removal of any pair from the precedence relation < makes the two processes
in the pair interfering processes.
Example
The system S = (P, <) is composed of the set of processes
P = { p1, ., p9 }
and the precedence relation
< = { (p1,p2), (p1,p3),
(p1,p4), (p2,p5), (p3,p5),
(p4,p6), (p4,p7),
(p4,p8), (p5,p8), (p6,p8),
(p7,p9), (p8,p9) }.
The processes have the following domains and ranges:
| process |
p1 | p2 | p3 |
p4 | p5 | p6 |
p7 | p8 | p9 |
|---|
| domain |
1 | 4 | 3 |
1 | 3 | 6 |
5 | 1,3 | 1,4,6 |
|---|
| range |
2,3 | 4 | 2,3 |
1 | 3 | 6 |
5 | 4 | 2,3 |
|---|
Transitive closure of <
In the following, a bullet is placed whenever the process in the row precedes
the process in the column under <.
| |
p1 | p2 | p3 |
p4 | p5 | p6 |
p7 | p8 | p9 |
|---|
| p1 |
| * | * |
* | | |
| | |
|---|
| p2 |
| | |
| * | |
| | |
|---|
| p3 |
| | |
| * | |
| | |
|---|
| p4 |
| | |
| | * |
* | * | |
|---|
| p5 |
| | |
| | |
| * | | |
|---|
| p6 |
| | |
| | |
| * | |
|---|
| p7 |
| | |
| | |
| | * |
|---|
| p8 |
| | |
| | |
| | * |
|---|
For p1, we have p1 < p2 and p2 < p5,
so p1 < p5. As p5 < p8, p1 <
p8. As p8 < p9, p1 < p9. The table
becomes:
| |
p1 | p2 | p3 |
p4 | p5 | p6 |
p7 | p8 | p9 |
|---|
| p1 |
| * | * |
* | * | |
| * | * |
|---|
| p2 |
| | |
| * | |
| | |
|---|
| p3 |
| | |
| * | |
| | |
|---|
| p4 |
| | |
| | * |
* | * | |
|---|
| p5 |
| | |
| | |
| * | | |
|---|
| p6 |
| | |
| | |
| * | |
|---|
| p7 |
| | |
| | |
| | * |
|---|
| p8 |
| | |
| | |
| | * |
|---|
Continuing on in this fashion, the table finally becomes:
| |
p1 | p2 | p3 |
p4 | p5 | p6 |
p7 | p8 | p9 |
|---|
| p1 |
| * | * |
* | * | * |
* | * | * |
|---|
| p2 |
| | |
| * | |
| * | * |
|---|
| p3 |
| | |
| * | |
| * | * |
|---|
| p4 |
| | |
| | * |
* | * | |
|---|
| p5 |
| | |
| | * |
* | * | * |
|---|
| p6 |
| | |
| | |
| * | * |
|---|
| p7 |
| | |
| | |
| | * |
|---|
| p8 |
| | |
| | |
| | * |
|---|
giving the transitive closure of < to be:
<* = { (p1,p2), (p1,p3), (p1,p4),
(p1,p5), (p1,p6), (p1,p7),
(p1,p8), (p1,p9), (p2,p5),
(p2,p8), (p2,p9), (p3,p5),
(p3,p8),
(p3,p9), (p4,p6), (p4,p7),
(p4,p8), (p4,p9), (p5,p8),
(p5,p9), (p6,p8), (p6,p9),
(p7,p9), (p8,p9) }
Bernstein Conditions
For the system to be determinate, the Bernstein conditions must hold. This
means that two processes which write into the same memory location cannot be
executed concurrently. Also, if a process reads from a location that another
process writes to, those two processes cannot be concurrent. So we first list
those processes which cannot be concurrent by computing the elements of the
three sets listed below. Note that the range of pi is the set of memory
locations that pi writes to, and the domain of pi is the set of
memory locations that pi reads from.
range(pi) INTERSECT range(pj) = { (p1,p3),
(p1,p5), (p1,p9), (p2,p8),
(p3,p5), (p3,p9), (p5,p9) }
domain(pi) INTERSECT range(pj) = { (p1,p4),
(p2,p8), (p3,p5), (p3,p9),
(p5,p9), (p8,p9) }
range(pi) INTERSECT domain(pj) = { (p1,p3),
(p1,p5), (p1,p8), (p2,p9),
(p3,p5), (p3,p8), (p4,p8),
(p4,p9), (p5,p8), (p6,p9) }
The Equivalent Maximally Parallel System
The only precedences that are actually required by the system are those
that enforce the Bernstein conditions. The complete set of precedences that
exist in the system is given by the set <*, so taking those elements of
<* in the three sets above gives us the precedence relation <+ for the
maximally parallel system equivalent to the original system:
<+ = { (p1,p3), (p1,p4), (p1,p5),
(p1,p8), (p1,p9), (p2,p8),
(p2,p9), (p3,p5), (p3,p8),
(p3,p9), (p4,p8), (p4,p9),
(p5,p8), (p5,p9),
(p6,p9), (p8,p9) }
Now, note that several of these elements are implied by others, since
precedence is transitive; for example, (p1,p4) and
(p4,p8) means (p1,p8) holds. Eliminating these
redundent precedences, this set becomes:
{ (p1,p3), (p1,p4), (p2,p8), (p3,p5), (p4,p8), (p5,p8), (p6,p9), (p8,p9) }
Bakery Algorithm
Introduction
This algorithm solves the critical section problem for n processes in
software. The basic idea is that of a bakery; customers take numbers, and
whoever has the lowest number gets service next. Here, of course, "service"
means entry to the critical section.
Algorithm
1 var choosing: shared array [0..n-1] of boolean;
2 number: shared array [0..n-1] of integer;
...
3 repeat
4 choosing[i] := true;
5 number[i] := max(number[0],number[1],...,number[n-1]) + 1;
6 choosing[i] := false;
7 for j := 0 to n-1 do begin
8 while choosing[j] do (* nothing *);
9 while number[j] <> 0 and
10 (number[j], j) < (number[i],i) do
11 (* nothing *);
12 end;
13 (* critical section *)
14 number[i] := 0;
15 (* remainder section *)
16 until false;
Comments
- lines 1-2:
- Here, choosing[i] is true if Pi is
choosing a number. The number that Pi will use to enter the critical
section is in number[i]; it is 0 if Pi is not
trying to enter its critical section.
- lines 4-6:
- These three lines first indicate that the process is choosing a
number (line 4), then try to assign a unique number to the process Pi
(line 5); however, that does not always happen. Afterwards, Pi
indicates it is done (line 6).
- lines 7-12:
- Now we select which process goes into the critical section.
Pi waits until it has the lowest number of all the processes waiting to
enter the critical section. If two processes have the same number, the one with
the smaller name - the value of the subscript - goes in; the notation
"(a,b) < (c,d)" means true if a <
c or if both a = c and b < d (lines
9-10). Note that if a process is not trying to enter the critical section, its
number is 0. Also, if a process is choosing a number when Pi tries to
look at it, Pi waits until it has done so before looking (line 8).
- line 14:
- Now Pi is no longer interested in entering its critical
section, so it sets number[i] to 0.
Bogus Bakery Algorithm
Introduction
Why does Lamport's Bakery algorithm used a variable called
choosing (see the algorithm, lines 1, 4, 6, and 8)? It is very
instructive to see what happens if you leave it out. This gives an example of
mutual exclusion being violated if you don't put choosing in.
But first, the algorithm (with the lines involving choosing
commented out) so you can see what the modification was:
Algorithm
1 var (* choosing: shared array [0..n-1] of boolean; *)
2 number: shared array [0..n-1] of integer;
...
3 repeat
4 (* choosing[i] := true; *)
5 number[i] := max(number[0],number[1],...,number[n-1]) + 1;
6 (* choosing[i] := false; *)
7 for j := 0 to n-1 do begin
8 (* while choosing[j] do ; *)
9 while number[j] <> 0 and
10 (number[j], j) < (number[i],i) do
11 (* nothing *);
12 end;
13 (* critical section *)
14 number[i] := 0;
15 (* remainder section *)
16 until false;
Proof of Violation of Mutual Exclusion
Suppose we have two processes just beginning; call them p0
and p1. Both reach
line 5 at the same time. Now, we'll assume both read number[0]
and number[1] before either addition takes place. Let
p1
complete the line, assigning 1 to number[1], but p0 block
before the assignment. Then p1 gets through the while loop at
lines 9-11 and enters the critical section. While in the critical section, it
blocks; p0 unblocks, and assigns 1 to number[0] at line 5. It
proceeds to the while loop at lines 9-11. When it goes through that loop for
j = 1, the condition on line 9 is true. Further, the condition
on line 10 is false, so p0 enters the critical section.
Now p0 and p1 are both
in the critical section, violating mutual exclusion.
The reason for choosing is to prevent the while
loop in lines 9-11 from being entered when process j is
setting its number[j]. Note that if the loop is entered
and then process j reaches line 5, one of two situations arises.
Either number[j] has the value 0 when the first test is
executed, in which case process i moves on to the next process, or
number[j] has a non-zero value, in which case at some
point number[j] will be greater than
number[i] (since process i finished executing
statement 5 before process j began). Either way, process i will
enter the critical section before process j, and when process j
reaches the while loop, it will loop at least until process
i leaves the critical section.
Test and Set Solution
Introduction
This algorithm solves the critical section problem for n processes using
a Test and Set instruction (called TaS here). This instruction does the
following function atomically:
function TaS(var Lock: boolean): boolean;
begin
TaS := Lock;
Lock := true;
end;
Algorithm
1 var waiting: shared array [0..n-1] of boolean;
2 Lock: shared boolean;
3 j: 0..n-1;
4 key: boolean;
...
5 repeat (* process Pi *)
6 waiting[i] := true;
7 key := true;
8 while waiting[i] and key do
9 key := TaS(Lock);
10 waiting[i] := false;
11 (* critical section goes here *)
12 j := i + 1 mod n;
13 while (j <> i) and not waiting[j] do
14 j := j + 1 mod n;
15 if j = i then
16 Lock := false
17 else
18 waiting[j] := false;
19 until false;
Comments
- lines 1-2:
- These are global to all processes, and are all initialized to
false.
- lines 3-4:
- These are local to each process Pi and are uninitialized.
- lines 5-10:
- This is the entry section. Basically,
waiting[i] is true as long as Pi is
trying to get into its critical section; if any other process is in that
section, then Lock will also be true, and Pi will loop
in lines 8-9. Once Pi can go on, it is no longer waiting for permission
to enter, and sets waiting[i] to false (line
10); it then proceeds into the critical section. Note that
Lock is set to true by the TaS
instruction in line 9 that returns false.
- lines 12-18:
- This is the exit section. When Pi leaves the critical
section, it must choose which other waiting process may enter next. It starts
with the process with the next higher index (line 12). It checks each process
to see if that process is waiting for access (lines 13-14); if no-one is, it
simply releases the lock (by setting Lock to false;
lines 15-16). However, if some other process Pj is waiting for entry,
Pi simply shanges waiting[j] to false to
allow Pj to enter the critical section (lines 17-18).
Classical Synchronization Problems
Introduction
This handout states three classical synchronization problems that are often
used to compare language constructs that implement synchronization mechanisms
and critical sections.
The Producer-Consumer Problem
In this problem, two processes, one called the producer and the other
called the consumer, run concurrently and share a common buffer. The
producer generates items that it must pass to the consumer, who is to consume
them. The producer passes items to the consumer through the buffer. However,
the producer must be certain that it does not deposit an item into the buffer
when the buffer is full, and the consumer must not extract an item from an
empty buffer. The two processes also must not access the buffer at the same
time, for if the consumer tries to extract an item from the slot into which the
producer is depositing an item, the consumer might get only part of the item.
Any solution to this problem must ensure none of the above three events
occur.
A practical example of this problem is electronic mail. The process you use to
send the mail must not insert the letter into a full mailbox (otherwise the
recipient will never see it); similarly, the recipient must not read a letter
from an empty mailbox (or he might obtain something meaningless but that looks
like a letter). Also, the sender (producer) must not deposit a letter in the
mailbox at the same time the recipient extracts a letter from the mailbox;
otherwise, the state of the mailbox will be uncertain.
Because the buffer has a maximum size, this problem is often called the
bounded buffer problem. A (less common) variant of it is the unbounded
buffer problem, which assumes the buffer is infinite. This eliminates the
problem of the producer having to worry about the buffer filling up, but the
other two concerns must be dealt with.
The Readers-Writers Problem
In this problem, a number of concurrent processes require access to some object
(such as a file.) Some processes extract information from the object and are
called readers; others change or insert information in the object and
are called writers. The Bernstein conditions state that many readers
may access the object concurrently, but if a writer is accessing the object, no
other processes (readers or writers) may access the object. There are two
possible policies for doing this:
First Readers-Writers Problem. Readers have priority over writers; that is,
unless a writer has permission to access the object, any reader requesting
access to the object will get it. Note this may result in a writer waiting
indefinitely to access the object.
Second Readers-Writers Problem. Writers have priority over readers; that is,
when a writer wishes to access the object, only readers which have already
obtained permission to access the object are allowed to complete their access;
any readers that request access after the writer has done so must wait until
the writer is done. Note this may result in readers waiting indefinitely to
access the object.
So there are two concerns: first, enforce the Bernstein conditions among the
processes, and secondly, enforcing the appropriate policy of whether the
readers or the writers have priority.
A typical example of this occurs with databases, when several processes are
accessing data; some will want only to read the data, others to change it. The
database must implement some mechanism that solves the readers-writers
problem.
The Dining Philosophers Problem
In this problem, five philosophers sit around a circular table eating spaghetti
and thinking. In front of each philosopher is a plate and to the left of each
plate is a fork (so there are five forks, one to the right and one to the left
of each philosopher's plate; see the figure). When a philosopher wishes to
eat, he picks up the forks to the right and to the left of his plate. When
done, he puts both forks back on the table. The problem is to ensure that no
philosopher will be allowed to starve because he cannot ever pick up both
forks.
There are two issues here: first, deadlock (where each philosopher picks up one
fork so none can get the second) must never occur; and second, no set of
philosophers should be able to act to prevent another philosopher from ever
eating. A solution must prevent both.
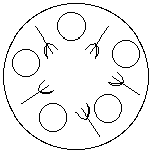
Figure. The Dining Philosopher's Table
Producer/Consumer Problem
Introduction
This algorithm uses semaphores to solve the producer/consumer (or bounded
buffer) problem.
Algorithm
1 var buffer: array [0..n-1] of item;
2 full, empty, mutex: semaphore;
3 nextp, nextc: item;
4 begin
5 full := 0;
6 empty := n;
7 mutex := 1;
8 parbegin
9 repeat (* producer process *)
10 (* produce an item in nextp *)
11 down(empty);
12 down(mutex);
13 (* deposit nextp in buffer *)
14 up(mutex);
15 up(full);
16 until false;
17 repeat (* consumer process *)
18 down(full);
19 down(mutex);
20 (* extract an item in nextc *)
21 up(mutex);
22 up(empty);
23 (* consume the item in nextc *)
24 until false;
25 parend;
26 end.
Comments
- lines 1-3
- Here, buffer is the shared buffer, and contains
n spaces; full is a semaphore the value of
which is the number of filled slots in the buffer, empty is a
semaphore the value of which is the number of emoty slots in the buffer, and
mutex is a semaphore used to enforce mutual exclusion (so only
one process can access the buffer at a time). nextp and
nextc are the items produced by the producer and consumed by
the consumer, respectively.
- line 5-7
- This just initializes all the semaphores. It is the only time
anything other than a down or an up operation may be done to
them.
- line 10
- Since the buffer is not accessed while the item is produced, we don't
need to put semaphores around this part.
- lines 11-13
- Depositing an item into the buffer, however, does require that the
producer process obtain exclusive access to the buffer. First, the producer
checks that there is an empty slot in the buffer for the new item and, if not,
waits until there is (down(empty)). When there is, it
waits until it can obtain exclusive access to the buffer
(down(mutex)). Once both these conditions are met, it
can safely deposit the item.
- lines 14-15
- As the producer is done with the buffer, it signals that any other
process needing to access the buffer may do so
(up(mutex)). It then indicates it has put another item
into the buffer (up(full)).
- lines 18-20
- Extracting an item from the buffer, however, does require that the
consumer process obtain exclusive access to the buffer. First, the consumer
checks that there is a slot in the buffer with an item deposited and, if not,
waits until there is (down(full)). When there is, it
waits until it can obtain exclusive access to the buffer
(down(mutex)). Once both these conditions are met, it
can safely extract the item.
- lines 21-22
- As the consumer is done with the buffer, it signals that any other
process needing to access the buffer may do so
(up(mutex)). It then indicates it has extracted another
item into the buffer (up(empty)).
- line 23
- Since the buffer is not accessed while the item is consumed, we don't
need to put semaphores around this part.
First Readers Writers Problem
Introduction
This algorithm uses semaphores to solve the first readers-writers problem.
Algorithm
1 var wrt, mutex: semaphore;
2 readcount: integer;
3 begin
4 readcount := 0;
5 wrt := 1;
6 mutex := 1;
7 parbegin
8 repeat (* reader process *)
9 (* do something *)
10 down(mutex);
11 readcount := readcount + 1;
12 if readcount = 1 then
13 down(wrt);
14 up(mutex);
15 (* read the file *)
16 down(mutex);
17 readcount := readcount - 1;
18 if readcount = 0 then
19 up(wrt);
20 up(mutex);
21 (* do something else *)
22 until false;
23 repeat (* writer process *)
24 (* do something *)
25 down(wrt);
26 (* write to the file *)
27 up(wrt);
28 (* do something else *)
29 until false;
30 parend;
31 end.
Comments
- lines 1-2
- Here, readcount contains the number of processes
reading the file, and mutex is a semaphore used to provide
mutual exclusion when readcount is incremented or decremented.
The semaphore wrt is common to both readers and writers and
ensures that when one writer is accessing the file, no other readers or writers
may do so.
- lines 4-6
- This just initializes all the semaphores. It is the only time
anything other than a down or an up operation may be done to
them. As no readers are yet reading the file, readcount is
initialized to 0.
- line 9
- Since the file is not accessed here, we don't need to put semaphores
around this part.
- lines 10-15
- Since the value of the shared variable readcount is
going to be changed, the process must wait until no-one else is accessing it
(down(mutex)). Since this process will read from the
file, readcount is incremented by 1; if this is the only reader
that will access the file, it waits until any writers have finished
(down(wrt)). It then indicates other processes may
access readcount (down(mutex)) and
proceeds to read from the file.
- lines 16-20
- Now the reader is done reading the file (for now.) It must update
the value of readcount to indicate this, so it waits until
no-one else is accessing that variable (down(mutex)) and
then decrements readcount. If no other readers are waiting to
read (readcount = 0), it signals that any reader or writer who
wishes to access the file may do so (up(wrt)).
Finally, it indicates it is done with readcount
(up(mutex)).
- line 24
- Since the file is not accessed here, we don't need to put semaphores
around this part.
- lines 25-26
- The writer process waits (down(wrt)) until
no other process is accessing the file; it then proceeds to write to the
file.
- line 27
- When the writer is done writing to the file, it signals that anyone who
wishes to access the file may do so (up(wrt)).
First Readers-Writers Problem
Introduction
This algorithm uses SP and SV to solve the first readers-writers
problem.
Algorithm
1 var mutex: semaphore;
2 readcount: integer;
3 begin
4 readcount := NREADERS;
5 mutex := 1;
6 parbegin
7 repeat (* reader process *)
8 (* do something *)
9 SP(readcount, 1, 1);
10 SP(mutex, 1, 0);
11 (* read the file *)
12 SV(readcount, 1);
13 (* do something else *)
14 until false;
15 repeat (* writer process *)
16 (* do something *)
17 SP(mutex, 1, 1; readcount, NREADERS, 0);
18 (* write to the file *)
19 SV(mutex, 1);
20 (* do something else *)
21 until false;
22 parend;
23 end.
Comments
- lines 1-2
- Here, readcount contains the number of processes not currently
reading (or trying to read) the file, and mutex is a semaphore used to
provide mutual exclusion when the file is being written.
- lines 3-5
- This just initializes all the semaphores. It is the only time
anything other than a P or a V operation may be done to them. As
no readers are yet trying to read the file, readcount is initialized to
the number of reader processes (the constant NREADERS).
- lines 7-8
- This first repeat loop contains the code for a reader
process. Since the file is not accessed here, we don't need to put semaphores
around this part.
- lines 9-11
- First we atomically decrement readcount by 1, since
a process is trying to read the file. We then check that no writers are
writing to the file by testing mutex. Note the value of mutex is
not changed.
- line 12
- Now the reader is done reading the file (for now.) It signals that one
less reader is (trying to) read the file by incrementing readcount by
1.
- lines 15-16
- This second repeat loop contains the code for a
writer process. Since the file is not accessed here, we don't need to put
semaphores around this part.
- lines 17-18
- The writer process waits until two conditions are met
simultaneously: no other writers are accessing the file (so mutex is
1, or false) and no readers are accessing the file (so
readcount is NREADERS). It then atomically sets mutex
to 0 (or true), indicating a writer process is accessing the file, but does not
change readcount.
- line 19
- When the writer is done writing to the file, it signals that anyone who
wishes to access the file may do so by making mutex 1, or
false.
General Priority Problem
Introduction
This uses SP and SV to solve the general priority problem, in
which many different processes each with a different priority is attempting to
gain access to a resource.
Algorithm
1 var resource: semaphore;
2 prisem: array[1..NUMPROCS] of semaphore;
3 begin
4 resource := 1;
5 for(i = 1; i <= NUMPROCS; i++)
6 prisem[i] := 1;
7 repeat (* the numproc'th process *)
8 (* do something *)
9 SP(prisem[numproc], 1, 1);
10 SP(resource, 1, 1;
11 prisem[0], 1, 0; ...; prisem[numproc-1], 1, 0);
12 (* access the resource *)
13 SV(resource, 1; prisem[numproc], 1);
14 (* do something else *)
15 until false;
16 ...
17 end.
Comments
- lines 1-2
- Here, resource is 1 when the resource is not being used, and
prisem[i] is 1 when process i does not want access to the
resource. We assume that the lower the index into prisem, the higher
the process priority.
- lines 3-6
- This just initializes all the semaphores. It is the only time
anything other than an SP or an SV operation may be done to them.
As the resource is not yet assigned, resource is set to 1
(false); as no process wants access to it, each semaphores
prisem[i] are also set to 1 (false).
- lines 7 on
- A liberty with notation now; this loop is replicated in each
process. We will assume that the variable procno contains the number of
the current process (that is, the index into prisem).
- line 8
- Since the resource is not accessed here, we don't need to put semaphores
around this part.
- lines 9-12
- First we atomically decrement
prisem[numproc] by 1, to indicate that
this process wishes to gain access to the resource. We then check atomically
(and simultaneously) that no other process has access, and that no process with
a higher priority is waiting for access. If these are both true, access to the
resource is granted, so resource is set to 0 (false), and the
process proceeds.
- line 13
- Now the process is done accessing the resource (for now.) It signals
that by setting both resource and the appropriate element of the
semaphore array to 1 (false).
send/receive Chart
Introduction
These charts summarize the actions of the send and receive primitives using
both blocking and non-blocking mode and explicit and implicit naming.
Charts
This
chart summarizes how naming and blocking affects the send primitive.
| send |
blocking |
non-blocking |
|---|
| explicit naming |
send message to receiver; wait until message accepted |
send message to receiver |
|---|
| implicit naming |
broadcast message; wait until all processes accept message |
broadcast message |
|---|
This
chart summarizes how naming and blocking affects the receive primitive.
| receive |
blocking |
non-blocking |
|---|
| explicit naming
| wait for message from named sender |
if there is a message from the named sender, get it; otherwise, proceed |
|---|
| implicit naming
| wait for message from any sender |
if there is a message from any sender, get it; otherwise, proceed |
|---|
Producer Consumer Problem
Introduction
This algorithm uses blocking send and receive primitives to solve the
producer/consumer (or bounded-buffer) problem. In this solution, the buffer
size depends on the capacity of the link.
Algorithm
1 var nextp, nextc: item;
2 procedure producer;
3 begin
4 while true do begin
5 (* produce item in nextp *)
6 send("Consumerprocess", nextp);
7 end;
8 end;
9 procedure consumer;
10 begin
11 while true do begin
12 receive("Producerprocess", nextc);
13 (* consume item in nextc *)
14 end;
15 end;
16 begin
17 parbegin
18 Consumerprocess: consumer;
19 Producerprocess: producer;
20 parend
21 end.
Comments
- line 1
- Here, nextp is the item the consumer produces, and
nextc the item that the consumer consumes.
- lines 2-8
- This procedure simply generates items and sends them to the consumer
process (named Consumerprocess). Suppose the capacity of the
link is n items. If n items are waiting to be consumed, and the
producer tries to send the n+1-st item, the producer will block
(suspend) until the consumer has removed one item from the link (i.e., done a
receive on the producer process). Note the name of the consumer process
is given explicitly, so this is an example of "explicit naming" or "direct
communication." Also, since the send is blocking, it ias an example of
"synchronous communication."
- lines 9-15
- This code simply receives items from the producer process (named
Producerprocess) and consumes them. If when the receive
statement is executed there are no items in the link, the consumer will block
(suspend) until the producer has put an item from the link (i.e., done a
send to the consumer process). Note the name of the producer process is
given explicitly; again this is an example of "explicit naming" or "direct
communication." Also, since the receive is blocking, it is an example
of "synchronous communication."
- lines 17-20
- This starts two concurrent processes, the
Consumerprocess and the Producerprocess.
Producer Consumer Problem
Introduction
This algorithm uses a monitor to solve the producer/consumer (or
bounded-buffer) problem.
Algorithm
1 buffer: monitor;
2 var slots: array [0..n-1] of item;
3 count, in, out: integer;
4 notempty, notfull: condition;
5 procedure entry deposit(data: item);
6 begin
7 if count = n then
8 notfull.wait;
9 slots[in] := data;
10 in := in + 1 mod n;
11 count := count + 1;
12 notempty.signal;
13 end;
14 procedure entry extract(var data: item);
15 begin
16 if count = 0 then
17 notempty.wait;
18 data := slots[out];
19 out := out + 1 mod n;
20 count := count - 1;
21 notfull.signal;
22 end;
23 begin
24 count := 0; in := 0; out := 0;
25 end.
Comments
- lines 2-4
- Here, slots is the actual buffer, count the number of items
in the buffer, and in and out the
indices of the next element of slots where a deposit is to be made or
from which an extraction is to be
made. There are two conditions we care about: if the buffer is not full
(represented by the condition
variable notfull), and if the buffer is not empty (represented by the
condition variable notempty).
- line 5
- The keyword entry means that this procedure may be called from
outside the monitor. It is
called by placing the name of the monitor first, then a period, then the
function name; so,
buffer.deposit(...).
- lines 7-8
- This code checks to see if there is room in the buffer for
a new item. If not, the process
blocks on the condition notfull; when some other process does extract an
element from the buffer, then
there will be room and that process will signal on the condition
notfull, allowing the blocked one to proceed.
Note that while blocked on this condition, other processes may access
procedures within the monitor.
- lines 9-11
- This code actually deposits the item into the buffer.
Note that the monitor guarantees
mutual exclusion.
- line 12
- Just as a producer will block on a full buffer, a consumer
will block on an empty one. This
indicates to any such consumer process that the buffer is no longer
empty, and unblocks exactly one of
them. If there are no blocked consumers, this is effectively a
no-op.
- line 14
- As with the previous procedure, this is called from outside
the monitor by
buffer.extract(...).
- lines 16-17
- This code checks to see if there is any unconsumed item
in the buffer. If not, the process
blocks on the condition notempty; when some other process does deposit
an element in the buffer, then
there will be something for the consumer to extract and that producer
process will signal on the condition
notempty, allowing the blocked one to proceed. Note that while blocked
on this condition, other processes
may access procedures within the monitor.
- lines 18-20
- This code actually extracts the item from the buffer.
Note that the monitor guarantees
mutual exclusion.
- line 21
- Just as a consumer will block on an empty buffer, a producer
will block on a full one. This
indicates to any such producer process that the buffer is no longer
full, and unblocks exactly one of them.
If there are no blocked producers, this is effectively a no-op.
- lines 23-25
- This is the initialization part.
First Readers Writers Problem
Introduction
This algorithm uses a monitor to solve the first readers-writers
problem.
Algorithm
1 readerwriter: monitor
2 var readcount: integer;
3 writing: boolean;
4 oktoread, oktowrite: condition;
5 procedure entry beginread;
6 begin
7 readcount := readcount + 1;
8 if writing then
9 oktoread.wait;
10 end;
11 procedure entry endread;
12 begin
13 readcount := readcount - 1;
14 if readcount = 0 then
15 oktowrite.signal;
16 end;
17 procedure entry beginwrite;
18 begin
19 if readcount > 0 or writing then
20 oktowrite.wait;
21 writing := true;
22 end;
23 procedure entry endwrite;
24 var i: integer;
25 begin
26 writing := false;
27 if readcount > 0 then
28 for i := 1 to readcount
29 oktoread.signal;
30 else
31 oktowrite.signal;
32 end;
33 begin
34 readcount := 0; writing := false;
35 end.
Comments
- lines 1-4
- Here, readcount contains the number of processes reading
the file, and writing is true when a
writer is writing to the file. Oktoread and oktowrite correspond to the
logical conditions of being able to
access the file for reading and writing, respectively.
- lines 7-9
- In this routine, the reader announces that it is ready to
read (by adding 1 to readcount). If a
writer is accessing the file, it blocks on the condition variable
oktoread; when done, the writer will signal
on that condition variable, and the reader can proceed.
- lines 13-15
- In this routine, the reader announces that it is done (by
subtracting 1 from readcount). If
no more readers are reading, it indicates a writer may go ahead by
signalling on the condition variable
oktowrite.
- lines 19-21
- In this routine, the writer first sees if any readers or
writers are accessing the file; if
so, it waits until they are done. Then it indicates that it is writing
to the file by setting the boolean writing
to true.
- lines 26-31
- Here, the writer first announces it is done by setting
writing to false. Since readers have
priority, it then checks to see if any readers are waiting; if so, it
signals all of them (as many readers can
access the file simultaneously). If not, it signals any writers
waiting.
- line 34
- This initializes the variables.
Monitors and Semaphores
Introduction
This handout describes how to express monitors in terms of semaphores.
If an operating system provided
semaphores as primitives, this is what a compiler would produce when
presented with a monitor.
Algorithm
1 var mutex, urgent, xcond: semaphore;
2 urgentcount, xcondcount: integer;
The body of each procedure in the monitor is set up like this:
3 down(xmutex);
4 (* procedure body*)
5 if urgentcount > 0 then
6 up(urgent)
7 else
8 up(mutex);
Each x.wait within the procedure is replaced by:
9 xcondcount := xcondcount + 1;
10 if urgentcount > 0 then
11 up(urgent)
12 else
13 up(mutex);
14 down(xcond);
15 xcondcount := xcondcount - 1;
Each x.signal within the procedure is replaced by:
16 urgentcount := urgentcount + 1;
17 if xcondcount > 0 then begin
18 up(xcondsem);
19 down(urgent);
20 end;
21 urgentcount := urgentcount - 1;
Comments
- line 1
- The semaphore mutex is initialized to 1 and ensures that only
one process at a time is executing
within the monitor. The semaphore urgent is used to enforce the
requirement that processes that signal
(and as a result are suspended) are to be restarted before any new
process enters the monitor. The
semaphore xcond will be used to block processes doing waits on the
condition variable x. Note that if there
is more than one such condition variable, a corresponding semaphore for
each condition variable must be
generated. Both urgent and xcond are initialized to 0.
- line 2
- The integer urgentcount indicates how many processes are
suspended as a result of a signal
operation (and are therefore waiting on the semaphore urgent); the
counter xcondcount is associated with
the condition variable x, and indicates how many processes are suspended
on that condition (i.e., suspended
on the semaphore xcond).
- lines 3-8
- Since only one process at a time may be in the monitor, the
process entering the monitor
procedure must wait until no other process is using it (down(mutex)).
On exit, the process signals others
that they may attempt entry, using the following order: if any other
process has issues a signal and been
suspended (i.e., urgentcount <> 0), the exiting process indicates that
one of those is to be continued
(up(urgent)). Otherwise, one of the processes trying to enter the
monitor may do so (up(mutex)).
- lines 9-15
- First, the process indicates it will be executing an
x.wait by adding 1 to xcondcount. It then
signals some other process that that process may proceed (using the same
priority as above). It suspends
on the semaphore xcond. When restarted, it indicates it is done with
the x.wait by subtracting 1 from
xcondcount, and proceeds. Note that the down(xcond) will always suspend
the process since, unlike
semaphores, if no process is suspended on x.wait, then x.signal is
ignored. So when this is executed, the
value of the semaphore xcond is always 0.
- lines 16-21
- First, the process indicates it will be executing an
x.signal by adding 1 to urgentcount. It
then checks if any process is waiting on condition variable x
(xcondcount > 0), and if so signals any such
process (up(xcondsem)) before suspending itself (down(urgent)). When
restarted, the process indicates it
is no longer suspended (by subtracting 1 from urgentcount).
Monitors and Priority Waits
Introduction
This is an example of a monitor using priority waits. It implements a
simple alarm clock; that is, a process
calls alarmclock.wakeme(n), and suspends for n seconds. Note that we
are assuming the hardware invokes
the procedure tick to update the clock every second.
Algorithm
1 alarmclock: monitor;
2 var now: integer;
3 wakeup: condition;
4 procedure entry wakeme(n: integer);
5 begin
6 alarmsetting := now + n;
7 while now < alarmsetting do
8 wakeup.wait(alarmsetting);
9 wakeup.signal;
10 end;
11 procedure entry tick;
12 begin
13 now := now + 1;
14 wakeup.signal;
15 end.
Comments
- lines 2-3
- Here, now is the current time (in seconds) and is updated
once a second by the procedure
tick. When a process suspends, it will do a wait on the condition
wakeup.
- line 6
- This computes the time at which the process is to be
awakened.
- lines 7-8
- The process now checks that it is to be awakened later, and
then suspends itself.
- line 9
- Once a process has been woken up, it signals the process that
is to resume next. That process
checks to see if it is time to wake up; if not, it suspends again (hence
the while loop above, rather than an if
statement). If it is to wake up, it signals the next process...
- line 14
- This is done once a second (hence the addition of 1 to now).
The processes to be woken up are
queued in order of remaining time to wait with the next one to wake up
first. So, when tick signals, the
next one to wake up determines if it is in fact time to wake up. If
not, it suspends itself; if so, it
proceeds.
First Readers Writers Problem
Introduction
This uses crowd monitors to solve the first readers/writers problem.
Algorithm
1 readerwriter: crowd monitor
2 var Readers: crowd read;
3 Writers: crowd read, write;
4 readcount: integer;
5 writing: boolean;
6 oktoread, oktowrite: condition;
7 guard procedure entry beginread;
8 begin
9 readcount := readcount + 1;
10 if writing then
11 oktoread.wait;
12 enter Readers;
13 end;
14 guard procedure entry endread;
15 begin
16 leave Readers;
17 readcount := readcount - 1;
18 if readcount = 0 then
19 oktowrite.signal;
20 end;
21 guard procedure entry beginwrite;
22 begin
23 if readcount > 0 or writing then
24 oktowrite.wait;
25 writing := true;
26 enter Writers;
27 end;
28 guard procedure entry endwrite;
29 var i: integer;
30 begin
31 leave Writers;
32 writing := false;
33 if readcount > 0 then
34 for i := 1 to readcount
35 oktoread.signal;
36 else
37 oktowrite.signal;
38 end;
39 procedure entry read;
40 ... read from shared data ...
41 end;
42 procedure entry write;
43 ... write to shared data ...
44 end;
45 begin
46 readcount := 0; writing := false;
47 end.
Comments
- lines 2-3
- These lines define which procedures can be called by members of the
crowd; here, members of the Readers crowd can call read, and
members of the Writers crowd can call either read or
write. Only processes in those crowds can call read or
write; should any other process do so, it will cause a run-time error.
- line 7
- The keyword guard means this procedure is mutually exclusive (so
only one process at a time may be in the guarded procedures). Note this
relaxes the definition of Hoare's monitor, in that multiple proceses may now
access the monitor simultaneously.
- line 12
- This puts the calling process into the Readers crowd; it may now
call the procedure read.
- line 16
- This removes the calling process from the Readers crowd, so it
may not call read until after it calls beginread and executes
line 12 again.
- line 26
- This puts the calling process into the Writers crowd; it may now
call the procedures read and write.
- line 31
- This removes the calling process from the Readers crowd, so it
may not call read or write until after it calls beginread
or beginwrite and executes lines 12 or 26 again.
- line 39
- Now any number of processes may access the read procedure
simultaneously.
- line 42
- Although it may appear that any number of processes may access the
write procedure simultaneously, note that all callers must first have
invoked beginwrite -- and only one such process will be active at a
time. So at most one process will call write.
Producer Consumer Problem
Introduction
This uses invariant expressions to solve the producer consumer problem.
Algorithm
1 buffer: invariant module;
2 const n = 1024;
3 var slots: array [0..n-1] of item;
4 in, out: 0..n-1;
5 invariant deposit
6 StartCount(deposit) - FinishCount(extract) < n;
7 CurrentCount(deposit) = 0;
8 invariant extract
9 StartCount(extract) - FinishCount(deposit) < 0
10 CurrentCount(extract) = 0;
11 procedure entry deposit(data: item);
12 begin
13 slots[in] := data;
14 in := in + 1 mod n;
15 end;
16 procedure entry extract(var data: item);
17 begin
18 data := slots[out];
19 out := out + 1 mod n;
20 end;
21 begin
22 in := 0; out := 0;
23 end.
Comments
- lines 3-4
- Here, slots is the actual buffer and in and out
the indices of the next element of slots where a deposit is to be made or from
which an extraction is to be made.
- line 5
- The next constraints apply to the procedure deposit.
- line 6
- his invariant checks that there is at least one slot in the buffer that
is empty. If false, then deposit must have been started at least
n times more than extract finished.
- line 7
- This ensures at most one process can be in deposit at a time
(mutual exclusion).
- line 8
- The next constraints apply to the procedure extract.
- line 9
- This invariant checks that there is at least one slot in the buffer that
is full. If so, then deposit finished more times than extract
started.
- line 10
- This ensures at most one process can be in extract at a time
(mutual exclusion).
- line 11
- As with the previous procedure, this is called from outside the monitor
by buffer.extract(...).
- lines 12-15
- This code actually extracts the item from the buffer. Note that
the invariant guarantees mutual exclusion.
lines 23-25
- This is the initialization part.
First Readers Writers Problem
Introduction
This uses invariant expressions to solve the first readers writers problem.
Algorithm
1 readerwriter: invariant module
2 invariant read
3 CurrentCount(write) = 0;
4 invariant write
5 CurrentCount(write) + CurrentCount(read) = 0;
6 procedure entry read;
7 ... read from shared data ...
8 end;
9 procedure entry write;
10 ... write to shared data ...
11 end;
12 begin
13 end.
Comments
- lines 2-3
- This states the condition that must hold whenever the procedure
read is executed; it requires that no processes be executing write.
Note this means readers will have priority over writers when a reader is
presently reading; it says nothing about what happens if a reader and a writer
call the module at the same time.
- lines 4-5
- This states the condition that must hold whenever the procedure
write is executed; it requires that no processes be executing either
read or write
- lines 6-11
- Here, the routines simply do the reading and writing.
- lines 12-13
- The initialization part of the module; as there are no variables in
it, this part is empty.
Producer Consumer Problem
Introduction
This algorithm uses open path expressions (in the form of Path Pascal) to solve
the producer/consumer problem.
Algorithm
1 type buffer: object;
2 path n:(1:(deposit); 1:(extract)) end;
3 var slots: array [0..n-1] of item;
4 in, out: integer;
5 procedure entry deposit(data: item);
6 begin
7 slots[in] := data;
8 in := in + 1 mod n;
9 end;
10 procedure entry extract(var data: item);
11 begin
12 data := slots[out];
13 out := out + 1 mod n;
14 end;
15 begin
16 in := 0; out := 0;
17 end.
Comments
- lines 1-2:
- This construct says that at most one invocation of deposit or
one invocation of extract can run concurrently (1:(...)), that
for every call to extract at least one call to deposit must have
returned, and that the difference between the number of calls to deposit
and the number of calls to extract must never be more than n.
- lines 3-4:
- Here, slots is the actual buffer, and in and
out the indices of the next element of slots where a deposit is
to be made or from which an extraction is to be made. Note that we need not
keep track of how many slots of the buffer contain something; the path
constraint above ensures that neither an extraction from an empty buffer nor
insertion into a full buffer will ever take place.
- line 5:
- This function is called by placing the name of the object first, then a
period, then the function name; so, buffer.deposit(...).
- lines 7-8:
- This code actually deposits the item into the buffer. Note that the
path expression guarantees mutual exclusion.
- line 10:
- Again, this is called by buffer.extract(...).
- line 14:
- This code actually extracts the item from the buffer. Again,the path
expression guarantees mutual exclusion.
Producer Consumer Process
Introduction
This uses Hoare's CSP language to solve the producer consumer problem.
Algorithm
This process manages the buffer; call it boundedbuffer.
1 buffer: (0..9) item;
2 in, out: integer;
3 in := 0;
4 out := 0;
5 *[in < out + n; producer ? buffer(in mod n)
6 -> in := in + 1
7 [] out < in; consumer ? more()
8 -> consumer ! buffer(out mod n);
9 out := out + 1
10 ]
Comments
- lines 1-2:
- Here, buffer is the buffer, in the number of items put
into the buffer, and out the number of items extracted. The producer
process outputs an item nextp to this process by:
bounded-buffer ! nextp;
and the consumer process outputs an item nextc to this process by:
bounded-buffer ! more(); bounded-buffer ? nextc;
(more() is there because CSP does not allow output commands in
guards.)
- lines 3-4:
- These just initialize in and out.
- lines 5-6:
- If there is room for another item in the buffer (in <
out + n), wait for the producer to produce something and deposit
it in an empty buffer slot (producer ? buffer(in
mod n)) and indicate that slot is now used (in :=
in + 1).
- lines 7-9:
- If the buffer is full (out < in), wait until the
consumer asks for something (consumer ? more()), then output the
next element of the buffer (consumer ! buffer(out
mod n)), and indicate it has been extracted (out :=
out + 1).
Producer Consumer Problem
Introduction
This algorithm uses ADA to solve the producer/consumer (or
bounded-buffer) problem.
Algorithm
This process (task, to ADA) manages the buffer.
1 task boundedbuffer is
2 entry deposit(data: in item);
3 entry extract(data: out item);
4 end;
5 task body boundedbuffer is
6 buffer: array[0..n-1] of item;
7 count: integer range 0..n := 0;
8 in, out: integer range 0..n-1 := 0;
9 begin
10 loop
11 select
12 when count < n =>
13 accept deposit(data: in item) do
14 buffer[in] := data;
15 end;
16 in := (in + 1) mod n;
17 count := count + 1;
18 or when count > 0 =>
19 accept extract(data: out item) do
20 data := buffer[out];
21 end;
22 out := (out + 1) mod n;
23 count := count - 1;
24 end select;
25 end loop;
26 end.
The producer deposits an item into the buffer with
27 boundedbuffer.deposit(nextp);
and the consumer extracts an item from the buffer with
28 boundedbuffer.extract(nextc);
Comments
- lines 1-4
- This indicates that the procedures deposit and extract may
be called outside the task, and
that extract will return something in its parameter list (the out).
- lines 6-8
- As usual, buffer is the buffer, and count the number of
items currently in the buffer; in and
out are the indices indicating where deposits go or where extractions
come from.
- lines 13-17
- If there is room in the buffer (when count < n) this
process will accept a request to
deposit an item in it (accept deposit ...); it then updates its
variables.
- lines 18-23
- If there is an item in the buffer (when count > 0)
this process will accept a request to
extract an item from the buffer (accept extract ...); the item is
returned via the parameter list. This
procedure then updates its variables.
- line 24
- If both of the above two when conditions are true, and both a
producer and consumer has
invoked a procedure named by an accept statement (called "an open
accept statement"), the
system will select one to be executed in some fair manner (such as
first-come-first-serve). If only one of
the conditions is true, and the procedure named in an accept statement
in the body of the when statement is
open, that one will be executed. If both of the when conditions are
false, an error condition occurs (this
usually terminates the process.)


